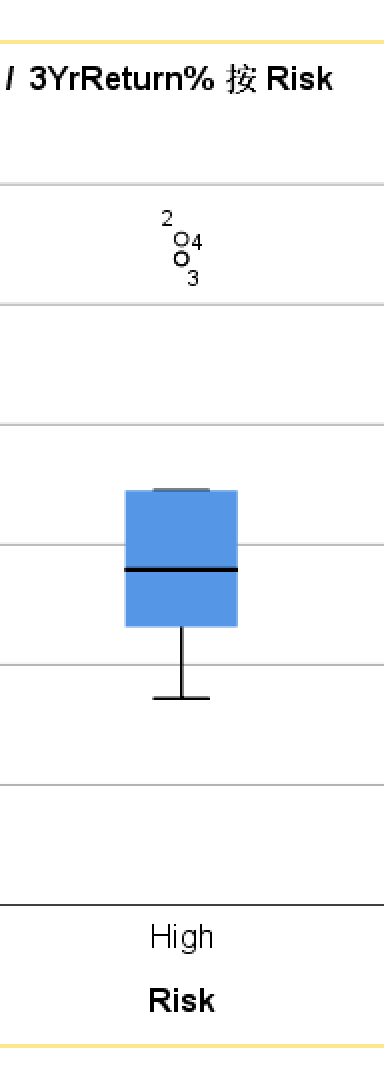
- 之前画箱线图发现有出现上箱比下箱长但上须却短得几乎看不见的情况(顶上还有几个远超上须上界的极端点)。老师没有在作业题中进行取对数的提示或者给出log(nYrReturn)的数据群,所以我猜想应当使用收益原数据进行箱线图的绘制。于是问了一下ds,自己又结合着数据和spss输出图想了一下,得出了以下结论。
-
首先还是从回顾箱线图的五个关键统计量开始:
1.Q1(下四分位数):数据中25%的值小于它。
2.Q2(中位数):数据中50%的值小于它。
3.Q3(上四分位数):数据中75%的值小于它。
4.IQR(四分位距):IQR = Q3 - Q1(上四-下四),代表了中间50%数据的范围。
5.须(Whisker):
· 上须:延伸到Q3+1.5IQR范围内的最大非异常值。(:注意!这里说的“上须延伸到的位置”是Q3+1.5IQR范围内的某个值,而不是Q3+1.5IQR这个值本身!)
· 下须:延伸到Q1-1.5IQR范围内的最小非异常值。(当然下须也是同理的。这个关键概念要厘清。)6.异常值(Outlier):超出须线范围的数据点,通常以点、星号等单独标记。(>Q3+1.5IQR或<Q1-1.5IQR的,就肯定不在箱和须线的范围内了。)
接下来思考一下可能导致题述此情况出现的原因:
· 上须短:(Q3,Q3+1.5IQR)之内的“正常右偏”数据点非常少(*翻译:绝绝绝大部分右偏数据都是“极端右偏”,即都比Q3+1.5IQR大很多),而在(Q3,Q3+1.5IQR)范围内的最大非异常值xn是紧挨着Q3的。这时候上须就被截断在这个最大非异常值xn处,使得上须(上须长=xn-Q3)看上去非常短。而那些异常值,用点或者星号标注到箱线图上,就只能在上须以上以上以上。
· 上箱长:由上箱长=Q3-Q2,下箱长=Q2-Q1,得出:上箱更长可能是因为Q3本身离中位数比Q1离中位数更远,这也就表明,数据上半部分本身的离散程度就更大。
因此,总体来看,这个上箱比下箱长、上须短得几乎“不可见”的箱线图,反映的数据应该具有这样的特征:
· 从整体上来看,这是一批在右侧长拖尾的数据。
· 从局部来看:
1.右拖尾,说明它的大部分数据集中在左侧;
2.上箱比下箱长,说明上四分位数偏离中位数比下四分位数偏离中位数的程度更大,即右侧数据比左侧数据离散程度更大;
3.上须极短,说明大部分右偏数据为“极端右偏”,而“正常右偏”的数据分布集中或极少,最重要的是它们与上四分位数相去不远;
4.顶上几个远超上须上界的点,说明其存在极端大值。
